(本题满分14分)已知函数f(x)=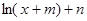
的图象在点(1，f(1))处的切线方程是
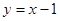，函数g(x)= 
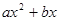(a、b∈R，a≠0)在x=2处取得极值-2．
(1)求函数f(x)、g(x)的解析式；
(2)若函数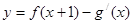
(其中
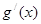是g(x)的导函数)在区间(
，
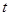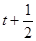)没有单调性，求实数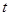的取值范围；
(3)设k∈Z，当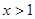
时，不等式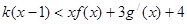
恒成立，求k的最大值．
推荐套卷
(本题满分14分)已知函数f(x)=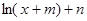的图象在点(1，f(1))处的切线方程是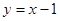，函数g(x)= 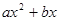(a、b∈R，a≠0)在x=2处取得极值-2．
(1)求函数f(x)、g(x)的解析式；
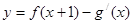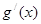(2)若函数(其中是g(x)的导函数)在区间(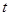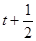，)没有单调性，求实数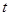的取值范围；
(3)设k∈Z，当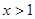时，不等式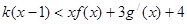恒成立，求k的最大值．
粤公网安备 44130202000953号