（本小题满分12分）编号分别为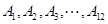
的
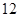名篮球运动员在某次篮球比赛中的得分记录如下:
（1）完成如下的频率分布表:
| 得分区间 |
频数 |
频率 |
 |
3 |
 |
 |
|
|
 |
|
|
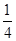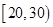| 合计 |
|
 |
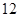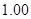（2）从得分在区间
内的运动员中随机抽取
人 ， 求这人得分之和大于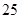
的概率.
满足
，
，且
，
。
的前
项和
．
的图象与
轴有两个不同公共点，若
,且当
时，
。
与
的大小。
，使得（1）
同时成立？若存在，求出
和
的值；若不存在，说明理由。
中，
，
表示
的直线交
于
,交
于
,且
，求证：
,求S的最大值。推荐套卷
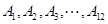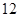（本小题满分12分）编号分别为的名篮球运动员在某次篮球比赛中的得分记录如下:
（1）完成如下的频率分布表:
| 得分区间 |
频数 |
频率 |
|
3 |
|
|
|
|
|
|
|
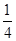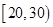| 合计 |
|
|
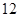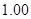（2）从得分在区间内的运动员中随机抽取人 ， 求这人得分之和大于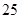的概率.
粤公网安备 44130202000953号