如图所示,在△ABC中,∠B=90º,△ABC三边长为整数且两直角边的长为关于 的一元二次方程
的一元二次方程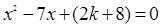 的两实数根,其中
的两实数根,其中 为正整数,且AB<BC
为正整数,且AB<BC

(1)求△ABC的三边长;
(2)点P从A点开始沿AB边向点B以1个单位长/秒的速度移动,而点Q从B点开始沿BC边向C以2个单位长/秒的速度移动,如果P,Q分别从A,B同时出发,经过几秒钟,△PBQ的面积为△ABC面积的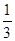 ?
?
相关知识点
推荐套卷
如图所示,在△ABC中,∠B=90º,△ABC三边长为整数且两直角边的长为关于 的一元二次方程
的一元二次方程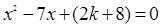 的两实数根,其中
的两实数根,其中 为正整数,且AB<BC
为正整数,且AB<BC

(1)求△ABC的三边长;
(2)点P从A点开始沿AB边向点B以1个单位长/秒的速度移动,而点Q从B点开始沿BC边向C以2个单位长/秒的速度移动,如果P,Q分别从A,B同时出发,经过几秒钟,△PBQ的面积为△ABC面积的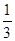 ?
?