在平面直角坐标系
中，正方形ABCD的位置如右图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第1个正方形的面积为 ；第n个正方形的面积为 ． 
相关试题
与边长为5的等边△AOB的边OA、AB分别相交于C、D两点，且OC＝3BD，则实数k的值为.
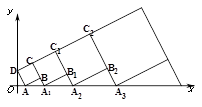
相关知识点
推荐套卷
在平面直角坐标系中，正方形ABCD的位置如右图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第1个正方形的面积为 ；第n个正方形的面积为 ．
粤公网安备 44130202000953号