综合实践活动课,某数学兴趣小组在学校操场上想测量汽车的速度,利用如下方法:如图,小王站在点处A(点A处)和公路(l)之间竖立着一块30m长且平行于公路的巨型广告牌(DE).广告牌挡住了小王的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.已知一辆匀速行驶的汽车经过公路BC段的时间是3s,已知小王到广告牌和公路的距离是分别是40m和80m,求该汽车的速度?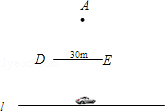
综合实践活动课,某数学兴趣小组在学校操场上想测量汽车的速度,利用如下方法:如图,小王站在点处A(点A处)和公路(l)之间竖立着一块30m长且平行于公路的巨型广告牌(DE).广告牌挡住了小王的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.已知一辆匀速行驶的汽车经过公路BC段的时间是3s,已知小王到广告牌和公路的距离是分别是40m和80m,求该汽车的速度?