如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C。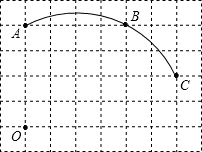
⑴请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，作出该圆弧所在圆的圆心D，并连接AD、CD。
⑵请在⑴的基础上，完成下列填空：
①写出点的坐标： C_______、D_______；
②直接写出⊙D半径＝_______（结果保留根号）；
③直接写出∠ADC＝_______；
④若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面的半径．
相关试题
已知抛物线
与抛物线
在直角坐标系中的位置如图所示，其中一条与
轴交于
，
两点．
（1）试判断哪条抛物线经过，两点，并说明理由；
（2）若，两点到原点的距离
，
满足条件
，求经过，两点的这条抛物线的函数式．
的图像，与
轴交于
，
两点，与
轴交于
点．
，
，
的符号，并说明理由；
，
，
，求这个二次函数的函数表达式．
．
为何实数，此二次函数的图像与
轴都有两个不同交点；
有最小值
，求函数表达式．
的顶点在抛物线
上，且抛物线在
轴上截得的线段长是
，求
和
的值．
与
的一些对应值：
，则当
？
的图象．相关知识点
推荐套卷
粤公网安备 44130202000953号