已知，如图，AB和DE是直立在地面上的两根立柱．AB=5m，某一时刻AB在阳光下的投影BC=3m．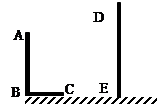
（1）请你在图中画出此时DE在阳光下的投影；
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长．
与7－
的值相等？
，
时，求
；
.相关知识点
推荐套卷
已知，如图，AB和DE是直立在地面上的两根立柱．AB=5m，某一时刻AB在阳光下的投影BC=3m．
（1）请你在图中画出此时DE在阳光下的投影；
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长．
粤公网安备 44130202000953号