图1是某城市四月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2.
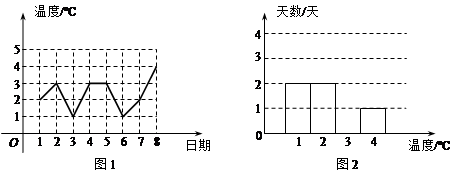
根据图中信息,解答下列问题:
(1)将图2补充完整;
(2)这8天的日最高气温的中位数是 ºC;
(3)计算这8天的日最高气温的平均数.
相关知识点
推荐套卷
图1是某城市四月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2.
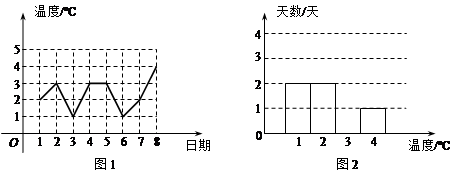
根据图中信息,解答下列问题:
(1)将图2补充完整;
(2)这8天的日最高气温的中位数是 ºC;
(3)计算这8天的日最高气温的平均数.