（本小题满分13分）已知椭圆
过点
，且与抛物线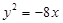
有一个公共的焦点.
（Ⅰ）求椭圆
方程；
（Ⅱ）斜率为
的直线
过椭圆的右焦点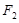
，且与椭圆交于
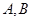两点，求弦
的长；
（Ⅲ）
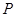为直线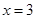
上的一点，在第（Ⅱ）题的条件下，若△
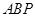为等边三角形，求直线的方程.
，
且圆心在直线
上的圆的方程．
； 
．
，
，在
轴上求点
，使
．
与已知圆
的交点，且在两坐标轴上的四个截距之和为
的圆的方程．
表示一个圆．
的取值范围；
的取值范围．推荐套卷
（本小题满分13分）已知椭圆过点，且与抛物线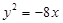有一个公共的焦点.
（Ⅰ）求椭圆方程；
（Ⅱ）斜率为的直线过椭圆的右焦点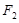，且与椭圆交于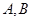两点，求弦的长；
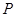（Ⅲ）为直线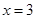上的一点，在第（Ⅱ）题的条件下，若△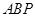为等边三角形，求直线的方程.
粤公网安备 44130202000953号