如图,直线y=x+2与抛物线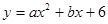 (a≠0)相交于A
(a≠0)相交于A 和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
相关知识点
推荐套卷
如图,直线y=x+2与抛物线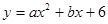 (a≠0)相交于A
(a≠0)相交于A 和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;