如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,﹣2).直线OM是一次函数y=x的图像.让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.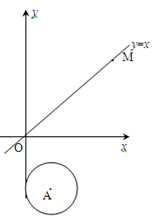
(1)填空
①直线OM与x轴所夹的锐角度数为 °;
②当t= 时,⊙A与坐标轴有两个公共点;
(2)当t>3时,求出运动过程中⊙A与直线OM相切时的t的值;
(3)运动过程中,当⊙A与直线OM相交所得的弦长为1时,求t的值.
相关知识点
推荐套卷
 为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.
为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.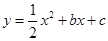 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),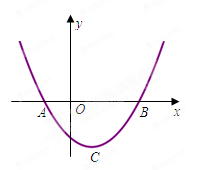

 3)改变动态关系,将静态问题升华为动态问题:
3)改变动态关系,将静态问题升华为动态问题: 后,再由小华随机取出一个小球,记下数字
后,再由小华随机取出一个小球,记下数字 为y.
为y.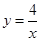 的图象上的概率;
的图象上的概率; 下方的概率.
下方的概率.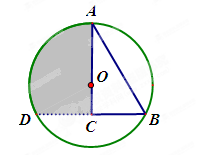
 =2CO ;
=2CO ; 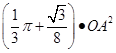
 粤公网安备 44130202000953号
粤公网安备 44130202000953号