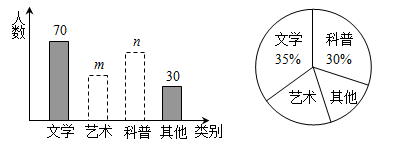
根据某网站调查，2014年网民们最关注的热点话题分别有：消费、教育、环保、反腐及其它共五类．根据调查的部分相关数据，绘制的统计图表如下
根据以上信息解答下列问题：
（1）请补全条形统计图并在图中标明相应数据；
（2）若北京市约有2100万人口，请你估计最关注环保问题的人数约为多少万人？
（3）在这次调查中，某单位共有甲、乙、丙、丁四人最关注教育问题，现准备从这四人中随机抽取两人进行座谈，则抽取的两人恰好是甲和乙的概率为 ．
（本小题满分8分）学校准备购买一批课外读物．学校就“我最喜爱的课外读物”从“文学”“艺术”“科普”和“其他”四个类别进行了抽样调查（每位同学只选一类），根据调查结果绘制的两幅不完整的统计图如下：
请你根据统计图提供的信息，解答下列问题：
（1）条形统计图中，m=，n=；
（2）扇形统计图中，艺术类读物所在扇形的圆心角是度；
（3）学校计划购买课外读物8000册，请根据样本数据，估计学校购买其他类读物多少册比较合理？
；
．如图，已知抛物线C1与坐标轴的交点依次是A（-4，0），B（-2，0），E（0，8）．
（1）求抛物线C1关于原点对称的抛物线C2的解析式；
（2）设抛物线C1的顶点为M，抛物线C2与x轴分别交于C，D两点（点C在点D的左侧），顶点为N，四边形MDNA的面积为S．若点A，点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动；与此同时，点M，点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动，直到点A与点D重合为止．求出四边形MDNA的面积S与运动时间t之间的关系式，并写出自变量t的取值范围；
（3）当t为何值时，四边形MDNA的面积S有最大值，并求出此最大值；
（4）在运动过程中，四边形MDNA能否形成矩形？若能，求出此时t的值；若不能，请说明理由．
（1）知识再现
如图（1）：若点A，B在直线l同侧，A，B到l的距离分别是3和2，AB="4，现在直线l上找一点P，使AP+BP的值最小，做法如下："
作点A关于直线l的对称点A′，连接BA′，与直线l的交点就是所求的点P，线段BA′的长度即为AP+BP的最小值，请你求出这个最小值．
（2）实践应用
①如图（2），⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC="60°P是OB上一动点" ，则PA+PC的最小值是
②如图（3），Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，
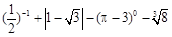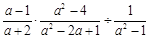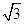），点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为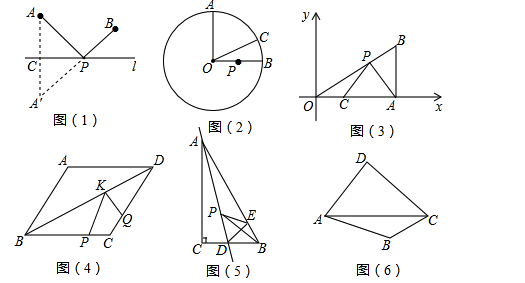
③如图（4），菱形ABCD中AB="2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点" ， 则PK+QK的最小值为
④如图（5），在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=，将△ACD沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是
（3）拓展延伸
如图（6）：在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD，保留作图痕迹，不必写出作法．
粤公网安备 44130202000953号