（本小题满分14分）如图，已知圆E:
，点
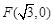，P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．
（Ⅰ）求动点Q的轨迹
的方程；
（Ⅱ）设直线
与(Ⅰ)中轨迹相交于
两点，直线
的斜率分别为
．△
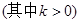的面积为
，以
为直径的圆的面积分别为
．若
恰好构成等比数列，求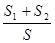
的取值范围．
相关试题
，
，求
取值范围；
的最值，并给出最值时对应的
的值．
,求
在点
处的切线方程；
，求函数
在
上的最大值和最小值．
满足
且
的单调增区间和值域 ．
的不等式
的解集为
，命题q：函数
为增函数．若
为真，
为假,求
的取值范围．
，
满足
．
，求
最小值．相关知识点
推荐套卷
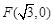（本小题满分14分）如图，已知圆E:，点，P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．
（Ⅰ）求动点Q的轨迹的方程；
（Ⅱ）设直线与(Ⅰ)中轨迹相交于两点，直线的斜率分别为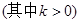．△的面积为，以为直径的圆的面积分别为．若恰好构成等比数列，求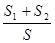的取值范围．
粤公网安备 44130202000953号