已知二次函数y=ax2+bx的图象经过点A（-5，0）和点B,其中点B在第一象限，且OA=OB，tan∠BAO=
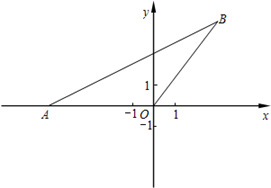
（1）求点B的坐标。
（2）求二次函数的解析式。
（3）过点B作直线BC平行于x轴，直线BC与二次函数图象的另一个交点为C，连结AC，如果点P在x轴上，且△ABC和△PAB相似，求点P的坐标。
相关试题
大15°，求这个角的度数．
．
=2-
．
）+5
×（-
）-0．25；
”，小黄误将
，求得结果是C．若
，
，请你帮助小明求出相关知识点
推荐套卷
已知二次函数y=ax2+bx的图象经过点A（-5，0）和点B,其中点B在第一象限，且OA=OB，tan∠BAO=
（1）求点B的坐标。
（2）求二次函数的解析式。
（3）过点B作直线BC平行于x轴，直线BC与二次函数图象的另一个交点为C，连结AC，如果点P在x轴上，且△ABC和△PAB相似，求点P的坐标。
粤公网安备 44130202000953号