（本小题满分12分）设抛物线C1:y2=4x的准线与x轴交于点F1，焦点为F2；以F1，F2为焦点，离心率为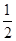
的椭圆记作C2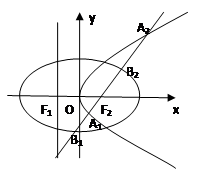
（1）求椭圆的标准方程；
（2）直线L经过椭圆C2的右焦点F2，与抛物线C1交于A1，A2两点，与椭圆C2交于B1，B2两点。当以B1B2为直径的圆经过F1时，求|A1A2|长。
（3）若M是椭圆上的动点，以M为圆心，MF2为半径作圆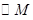
,是否存在定圆
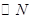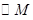,使得与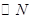恒相切？若存在，求出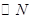的方程，若不存在，请说明理由。
相关试题
=
是矩阵M=
属于特征值λ1=2的一个特征向量．
，求M10a．选修4﹣2：矩阵与变换
已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量
=（
），并有特征值λ2=﹣1及属于特征值﹣1的一个特征向量
=（
），
=（
）．
（1）求矩阵M；
（2）求M5α．
，
；求A4B．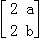
的两个特征值分别为λ1=﹣1和λ2=4．
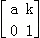（k≠0）的一个特征向量为
=
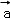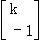，矩阵A的逆矩阵A﹣1对应的变换将点（3，1）变为点（1，1）．相关知识点
推荐套卷
粤公网安备 44130202000953号