甲、乙两车分别从相距200千米的A、B两地同时出发相向而行，甲到B地后立即返回，乙到A地后停止行驶，下图是它们离各自出发地的距离y（km）与行驶时间x（h）之间的函数图象．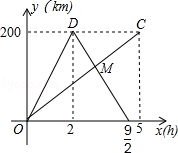
（1）请直接写出甲离出发地A的距离y（km）与行驶时间x（h）之间的函数关系式，并写出自变量x的取值范围；
（2）求出函数图象交点M的坐标并指出该点坐标的实际意义；
（3）求甲、乙两车从各自出发地驶出后经过多长时间相遇．
相关试题
，其中
．
中，
，
是
的中点，连接
．
，
，
是垂足．图中共有多少对全等三角形？请直接用“
”符号把它们分别表示出来（不要求证明）．
如图，一抛物线经过点A（−2，0），点B（0，4）和点C（4，0），该抛物线的顶点为D．
（1）求该抛物线的函数关系式及顶点D坐标．
（2）如图，若P为线段CD上的一个动点，过点P作PM⊥x轴于点M，求四边形PMAB的面积的最大值和此时点P的坐标．
（3）过抛物线顶点D，作DE⊥x轴于E点，F（m，0）是x轴上一动点，若以BF为直径的圆与线段DE有公共点，求m的取值范围．
粤公网安备 44130202000953号