已知数轴上有A、B、C三点，分别表示有理数-26，-10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．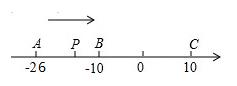
（1）用含t的代数式表示P到点A和点C的距离：PA=________，PC=_____________
（2）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回点A，当点Q开始运动后，请用t的代数式表示P、Q两点间的距离。（友情提醒：注意考虑P、Q的位置）
相关试题
已知数轴上有A、B、C三点，分别表示有理数-26，-10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．
（1）用含t的代数式表示P到点A和点C的距离：PA=________，PC=_____________
（2）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回点A，当点Q开始运动后，请用t的代数式表示P、Q两点间的距离。（友情提醒：注意考虑P、Q的位置）
＝－
，其中
粤公网安备 44130202000953号