高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点突发火灾,消防队必须立即赶往救火,已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?说明理由.(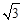 取1.732)
取1.732)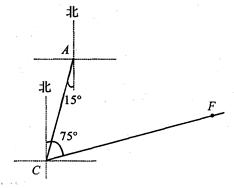
相关知识点
推荐套卷
高考英语听力测试期间,需要杜绝考点周围的噪音,如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点突发火灾,消防队必须立即赶往救火,已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?说明理由.(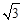 取1.732)
取1.732)