如图1,在平面直角坐标系中,点M在x轴的正半轴上,⊙M交x轴 于A、B两点,交y轴C、D于两点,且C为弧AE的中点,AE交y轴于点G,若A点的坐标为(-2,0),CD=8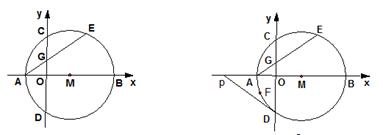
(1)求⊙M的半径
(2)求AE的长
(3)如图2,过点D作⊙M的切线,交x轴于点P.动点F在⊙M圆周上运动时, 的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
推荐套卷
如图1,在平面直角坐标系中,点M在x轴的正半轴上,⊙M交x轴 于A、B两点,交y轴C、D于两点,且C为弧AE的中点,AE交y轴于点G,若A点的坐标为(-2,0),CD=8
(1)求⊙M的半径
(2)求AE的长
(3)如图2,过点D作⊙M的切线,交x轴于点P.动点F在⊙M圆周上运动时, 的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律