某餐厅中1张餐桌可坐6人，有以下两种摆放方式：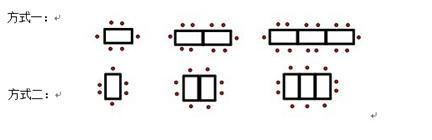
（1）对于方式一，4张桌子拼在一起可坐多少人？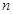
张桌子呢？对于方式二呢？
（2）该餐厅有40张这样的长方形桌子，按方式一每5张拼成一张大桌子，则40张桌子可拼成8张大桌子，共可坐多少人？按方式二呢？
（3）在（2）中，若改成每8张拼成一张大桌子，则共可坐多少人？
（4）一天中午，该餐厅来了98为顾客共同就餐，但餐厅中只有25张这样的长方形桌子可用，若你是这家餐厅的经理，你打算选择哪种方式来摆餐桌呢？
相关试题
为美化青岛，创建文明城市，园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配
、
两种园艺造型共50个，摆放在迎宾大道两侧．搭配每个造型所需花卉情况如右表所示：
结合上述信息，解答下列问题：
（1）符合题意的搭配方案有哪几种?
（2）若搭配一个种造型的成本为1000元，搭配一个种造型的成本为1200元，试说明选用（1）中哪种方案成本最低？
南宁市是广西最大的罗非鱼养殖产区，被国家农业部列为罗非鱼养殖优势区域．某养殖场计划下半年养殖无公害标准化罗非鱼和草鱼，要求这两个品种总产量
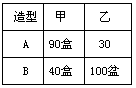
（吨）满足：
，总产值为1000万元．已知相关数据如右表所示．
| 品种 |
单价（万元/吨） |
| 罗非鱼 |
0.45 |
| 草鱼 |
0.85 |
求：该养殖场下半年罗非鱼的产量应控制在什么范围？（产值＝产量
单价）
并将解集在数轴上表示出来.
售价
成本）相关知识点
推荐套卷
粤公网安备 44130202000953号