设函数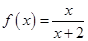 (x>0),观察:
(x>0),观察: ,f2(x)=f(f1(x))=
,f2(x)=f(f1(x))= 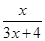 ,
,
f3(x)=f(f2(x))=  ,f4(x)=f(f3(x))=
,f4(x)=f(f3(x))= 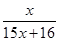 ,……
,……
根据以上事实,由归纳推理可得:当n∈N*且n≥2时,fn(x)=f(fn-1(x))= .
相关知识点
推荐套卷
设函数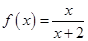 (x>0),观察:
(x>0),观察: ,f2(x)=f(f1(x))=
,f2(x)=f(f1(x))= 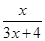 ,
,
f3(x)=f(f2(x))=  ,f4(x)=f(f3(x))=
,f4(x)=f(f3(x))= 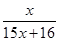 ,……
,……
根据以上事实,由归纳推理可得:当n∈N*且n≥2时,fn(x)=f(fn-1(x))= .