在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为
（米/单位时间）,单位时间内用氧量为
（
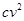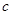为正常数）;②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为
（米/单位时间）, 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为
.
（1）将表示为的函数;
（2）设0<≤5,试确定下潜速度,使总的用氧量最少.
相关试题
的奇偶性。 (2)判断函数
的定义域：
，当
时f(x)>0，
时f(x)<0
的解集为R.
t + 30 (1 ≤ t ≤ 30 , t ∈ N )，后20天价格为g (t) =" 45" (31 ≤ t ≤ 50 , t ∈ N )．推荐套卷
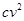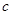在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为（米/单位时间）,单位时间内用氧量为（为正常数）;②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为（米/单位时间）, 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为.
（1）将表示为的函数;
（2）设0<≤5,试确定下潜速度,使总的用氧量最少.
粤公网安备 44130202000953号