在数学课的学习中,我们已经接触了很多代数恒等式,知道可以用图形的面积来解释这些代数恒等式.如图①可以解释恒等式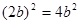 ;
; 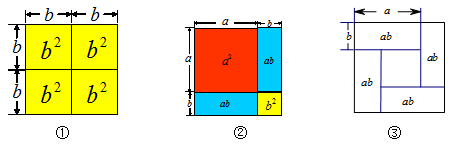
(1)如图②可以解释恒等式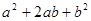 = .
= .
(2)如图③是由4个长为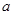 ,宽为
,宽为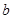 的长方形纸片围成的正方形,
的长方形纸片围成的正方形,
①用面积关系写出一个代数恒等式: .
②若长方形纸片的面积为3,且长比宽长3,求长方形的周长(其中a.b都是正数,结果可保留根号)
相关知识点
推荐套卷
 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍。
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍。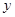 轴对称,过H作⊙O切线交
轴对称,过H作⊙O切线交
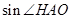 的值;
的值;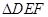 是以EF为底的等腰三角形,试探索
是以EF为底的等腰三角形,试探索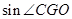 的大小怎样变化?请说明理由。
的大小怎样变化?请说明理由。

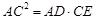 ;
; 的值。
的值。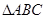 中,
中,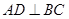 于点D,
于点D,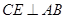 于点E,
于点E,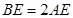 ,
,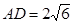 ,
,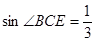 ,求CE的长。
,求CE的长。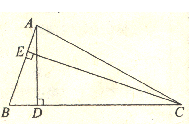
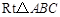 中,
中,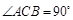 ,
, ,
,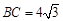 ,以
,以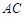 为直径的⊙O交
为直径的⊙O交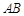 于点
于点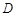 ,点
,点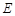 是
是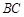 的中点,OB,DE相交于点F。
的中点,OB,DE相交于点F。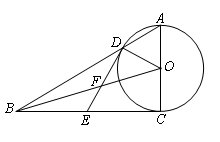
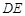 是⊙O的切线;
是⊙O的切线; 粤公网安备 44130202000953号
粤公网安备 44130202000953号