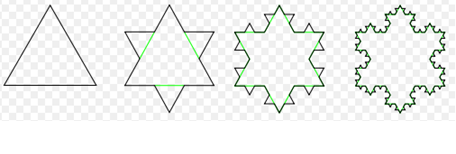
如图是瑞典人科赫(Koch)在1906年构造的能够描述雪花形状的科赫雪花图案.图形的作法是,从一个正三角形开始,把每条边分成三等份,然后以各边的中间长度为底边.分别向外作正三角形,再把“底边”线段抹掉.反复进行这一过程,就会得到一个“雪花”样子的曲线.这是一个极有特色的图形:在图形不断变换的过程中,它的周长趋于无穷大,而其面积却趋于定值.如果假定原正三角形边长为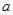 ,则可算出下图每步变换后科赫雪花的周长:
,则可算出下图每步变换后科赫雪花的周长: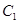 =3
=3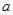 ,
,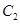 = ,
= , = ,…,则
= ,…,则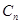 = .
= .
相关知识点
推荐套卷
 +(y+2)2=0,则yx=.
+(y+2)2=0,则yx=.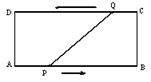
 ,且与O相距6km的Q处.如图所示.货船的航行速度是____________km/h.(结果用根号表示.)
,且与O相距6km的Q处.如图所示.货船的航行速度是____________km/h.(结果用根号表示.)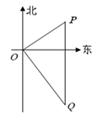
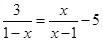 的解是___________.
的解是___________. 粤公网安备 44130202000953号
粤公网安备 44130202000953号