如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.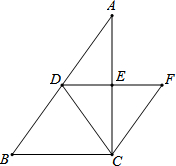
(1)求证:DE=EF;
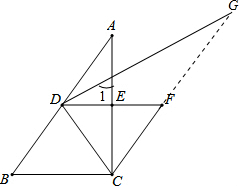
(2)连接CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.
相关知识点
推荐套卷
如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.

(1)求证:DE=EF;
(2)连接CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.