设不等式组
所表示的平面区域为Dn，记Dn内整点的个数为an（横纵坐标均为整数的点称为整点）．
（1）n＝2时，先在平面直角坐标系中作出区域D2，再求a2的值；
（2）求数列{an}的通项公式；
（3）记数列{an}的前n项的和为Sn，试证明：对任意n∈N*,
恒有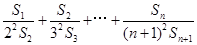
<
成立．
，
的图象；
（2）
（2）
，若
，
的值。
上有意义的两个函数
如果有任意
则称
与
在
与
给定区间
， 讨论
与
在给定区间推荐套卷
设不等式组所表示的平面区域为Dn，记Dn内整点的个数为an（横纵坐标均为整数的点称为整点）．
（1）n＝2时，先在平面直角坐标系中作出区域D2，再求a2的值；
（2）求数列{an}的通项公式；
（3）记数列{an}的前n项的和为Sn，试证明：对任意n∈N*,
恒有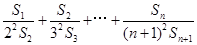<成立．
粤公网安备 44130202000953号