(有难度哦)给定有限单调递增数列
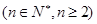 且
且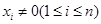 ,定义集合
,定义集合 且
且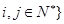 .若对任意点
.若对任意点 ,存在点
,存在点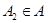 使得
使得 (
( 为坐标原点),则称数列
为坐标原点),则称数列 具有性质
具有性质 .
.
(Ⅰ)判断数列 :
: 和数列
和数列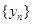 :
: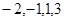 是否具有性质
是否具有性质 ,简述理由.
,简述理由.
(Ⅱ)若数列 具有性质
具有性质 ,求证:
,求证:
①数列 中一定存在两项
中一定存在两项 使得
使得 ;
;
②若 ,
,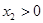 且
且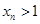 ,则
,则 .
.
推荐套卷
(有难度哦)给定有限单调递增数列
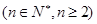 且
且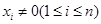 ,定义集合
,定义集合 且
且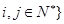 .若对任意点
.若对任意点 ,存在点
,存在点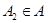 使得
使得 (
( 为坐标原点),则称数列
为坐标原点),则称数列 具有性质
具有性质 .
.
(Ⅰ)判断数列 :
: 和数列
和数列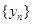 :
: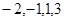 是否具有性质
是否具有性质 ,简述理由.
,简述理由.
(Ⅱ)若数列 具有性质
具有性质 ,求证:
,求证:
①数列 中一定存在两项
中一定存在两项 使得
使得 ;
;
②若 ,
,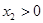 且
且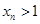 ,则
,则 .
.