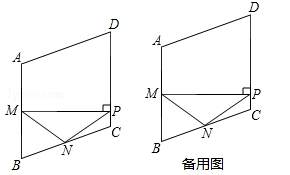
等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
相关知识点
推荐套卷
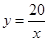 (
(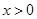 )的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线
)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线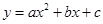 经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.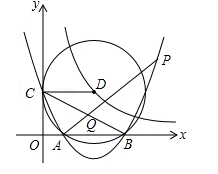
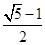 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.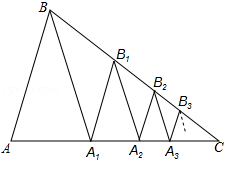
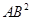 =AA1•A C;
=AA1•A C;
 ,求m的値:
,求m的値: DQ的最大值.
DQ的最大值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号