如图甲,已知ΔABC和ΔCEF是两个不等的等边三角形,且有一个公共顶点C,连接AF和BE.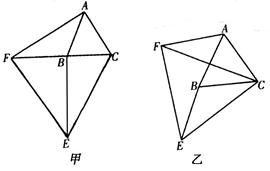
(1)线段AF和BE有怎样的大小关系?证明你的猜想.
(2)将图中的ΔCEF绕点C旋转一定的角度,得到图乙,(1)中的结论还成立吗? 做出判断并说明理由.
推荐套卷
如图甲,已知ΔABC和ΔCEF是两个不等的等边三角形,且有一个公共顶点C,连接AF和BE.
(1)线段AF和BE有怎样的大小关系?证明你的猜想.
(2)将图中的ΔCEF绕点C旋转一定的角度,得到图乙,(1)中的结论还成立吗? 做出判断并说明理由.