根据条件求函数解析式：（6分× 2 = 12分）
（1）已知一抛物线与x轴的交点是A(－2，0)、B（1，0），且经过点C（2，8），求该抛物线的解析式；
（2）抛物线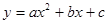
经过A（1，4）、B（-1，0）、C（-2，7）三点，求抛物线的解析式．
相关知识点
推荐套卷
根据条件求函数解析式：（6分× 2 = 12分）
（1）已知一抛物线与x轴的交点是A(－2，0)、B（1，0），且经过点C（2，8），求该抛物线的解析式；
（2）抛物线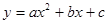经过A（1，4）、B（-1，0）、C（-2，7）三点，求抛物线的解析式．
粤公网安备 44130202000953号