已知椭圆C: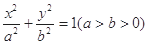 ,⊙
,⊙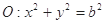 , 点
, 点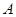 ,
,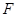 分别是椭圆
分别是椭圆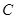 的左顶点和左焦点,点
的左顶点和左焦点,点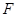 不是
不是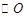 上的点,点
上的点,点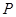 是
是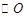 上的动点.
上的动点.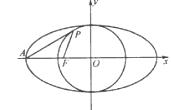
(1)若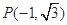 ,
,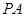 是
是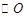 的切线,求椭圆
的切线,求椭圆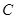 的方程;
的方程;
(2)是否存在这样的椭圆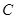 ,使得
,使得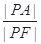 恒为常数?如果存在,求出这个数及
恒为常数?如果存在,求出这个数及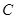 的离心率
的离心率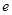 ;如果不存在,说明理由.
;如果不存在,说明理由.
推荐套卷
已知椭圆C: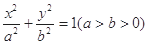 ,⊙
,⊙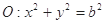 , 点
, 点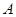 ,
,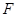 分别是椭圆
分别是椭圆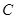 的左顶点和左焦点,点
的左顶点和左焦点,点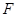 不是
不是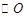 上的点,点
上的点,点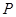 是
是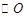 上的动点.
上的动点.
(1)若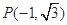 ,
,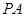 是
是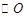 的切线,求椭圆
的切线,求椭圆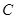 的方程;
的方程;
(2)是否存在这样的椭圆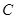 ,使得
,使得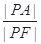 恒为常数?如果存在,求出这个数及
恒为常数?如果存在,求出这个数及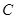 的离心率
的离心率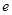 ;如果不存在,说明理由.
;如果不存在,说明理由.