在一次自主招生选拔考核中，每个候选人都需要进行四轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰，已知某候选人能正确回答第一，二，三，四轮问题的概率分别为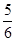
，
，
，
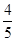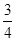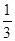，且各轮问题能否正确回答互不影响．
（1）求该选手进入第三轮才被淘汰的概率；
（2）该选手在选拔过程中回答问题的个数记为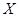
，求随机变量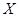的分布列和期望．
相关试题
．
是偶函数，求出的实数
的值；
有两解，求出实数
，记
，试求函数
在区间
上的最大值.
．
时，求函数
的最大值；
上的任意一个
，都有
成立，求实数
的取值范围．
（其中
的图象与
轴的交点中，相邻两个交点之间的距离为
，且图象上一个最低点为
．（1）求
的解析式；（2）当
时，求
，
．
在
上的图像；（2）求函数
．
；
，求推荐套卷
在一次自主招生选拔考核中，每个候选人都需要进行四轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰，已知某候选人能正确回答第一，二，三，四轮问题的概率分别为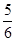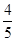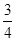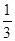，，，，且各轮问题能否正确回答互不影响．
（1）求该选手进入第三轮才被淘汰的概率；
（2）该选手在选拔过程中回答问题的个数记为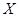，求随机变量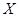的分布列和期望．
粤公网安备 44130202000953号