如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.
(1)搭n条小鱼需要火柴棒 根;
(2)计算搭12条小鱼需要多少根火柴棒?
(3)若搭n朵某种小花需要火柴棒(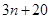 )根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.
(1)搭n条小鱼需要火柴棒 根;
(2)计算搭12条小鱼需要多少根火柴棒?
(3)若搭n朵某种小花需要火柴棒(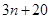 )根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.