已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．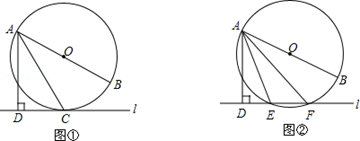
（1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．
，其中
．
，其中
；
．
；
；相关知识点
推荐套卷
已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．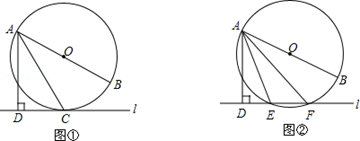
（1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．
粤公网安备 44130202000953号