下列命题:①数列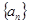 为递减的等差数列且
为递减的等差数列且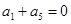 ,设数列
,设数列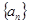 的前
的前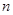 项和为
项和为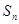 ,则当
,则当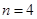 时,
时,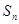 取得最大值;②设函数
取得最大值;②设函数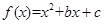 ,则
,则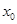 满足关于
满足关于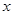 的方程
的方程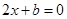 的充要条件是对任意
的充要条件是对任意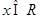 均有
均有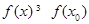 ;③在长方体
;③在长方体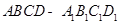 中,
中,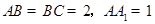 ,直线
,直线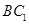 与平面
与平面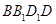 所成角的正弦值为
所成角的正弦值为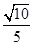 ;④定义在
;④定义在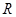 上的函数
上的函数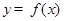 满足
满足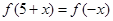 且
且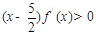 ,已知
,已知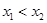 ,则
,则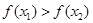 是
是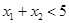 的充要条件.
的充要条件.
其中正确命题的序号是 (把所有正确命题的序号都写上).
推荐套卷
下列命题:①数列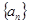 为递减的等差数列且
为递减的等差数列且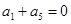 ,设数列
,设数列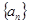 的前
的前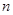 项和为
项和为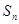 ,则当
,则当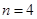 时,
时,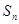 取得最大值;②设函数
取得最大值;②设函数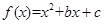 ,则
,则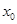 满足关于
满足关于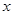 的方程
的方程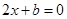 的充要条件是对任意
的充要条件是对任意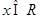 均有
均有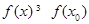 ;③在长方体
;③在长方体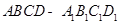 中,
中,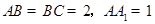 ,直线
,直线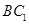 与平面
与平面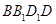 所成角的正弦值为
所成角的正弦值为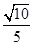 ;④定义在
;④定义在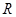 上的函数
上的函数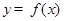 满足
满足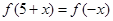 且
且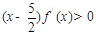 ,已知
,已知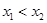 ,则
,则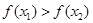 是
是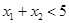 的充要条件.
的充要条件.
其中正确命题的序号是 (把所有正确命题的序号都写上).