随着我国人民生活水平和质量的提高,百岁寿星日益增多.某市是中国的长寿之乡,截至2008年2月底,该市五个地区的100周岁以上的老人分布如下表(单位:人):
 地区 地区
性别
|
一
|
二
|
三
|
四
|
五
|
男性
|
21
|
30
|
38
|
42
|
20
|
女性
|
39
|
50
|
73
|
70
|
37
|
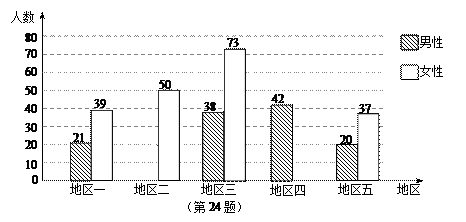
根据表格中的数据得到条形图如下:
解答下列问题:
(1)请把统计图中地区二和地区四中缺失的数据、图形补充完整;
(2)填空:该市五个地区100周岁以上老人中,男性人数的极差是人,女性人数的中位数是人;
(3)预计2015年该市100周岁以上的老人将比2008年2月的统计数增加100人,请你估算2015年地区一增加100周岁以上的男性老人多少人?