我县实施新课程改革后,学生的自主学习、合作交流能力有很大提高,胡老师为了了解班级学生自主学习、合作交流的具体情况,对某班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

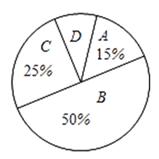
(1)本次调查中,胡老师一共调查了 _________ 名同学,其中女生共有 _________ 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,胡老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.