先阅读，再回答问题：如图1，已知△ABC中，AD为中线．延长AD至E，使DE=AD．在△ABD和△ECD中，AD=DE，∠ADB=∠EDC，BD=CD，所以，△ABD≌△ECD（SAS），进一步可得到AB=CE，AB∥CE等结论．
在已知三角形的中线时，我们经常用“倍长中线”的辅助线来构造全等三角形，并进一步解决一些相关的计算或证明题．
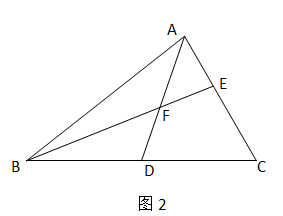
解决问题：如图2，在△ABC中，AD是三角形的中线，F为AD上一点，且BF=AC，连结并延长BF交AC于点E，求证：AE=EF．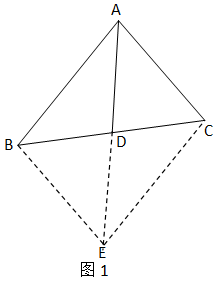
相关试题
为
的直径，
交
，
交
．
的度数；
．某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放量的破裂管道有水部分的截面．
（1）请你补全这个输水管道的圆形截面；（尺规作图）
（2）若这个输水管道有水部分的水面宽AB="16" cm，水面最深地方的高度为4 cm，求这个圆形截面的半径．
的一元二次方程
的一个根是
，求另一个根及k的值．
相关知识点
推荐套卷
粤公网安备 44130202000953号