如图，从原点A开始，以AB＝1为直径画半圆，记为第1个半圆；以BC＝2为直径画半圆，记为第2个半圆；以CD＝4为直径画半圆，记为第3个半圆；以DE＝8为直径画半圆，记为第4个半圆；···，按此规律，继续画半圆，则第6个半圆的面积为______________．（结果保留π）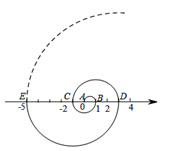
相关知识点
推荐套卷
如图，从原点A开始，以AB＝1为直径画半圆，记为第1个半圆；以BC＝2为直径画半圆，记为第2个半圆；以CD＝4为直径画半圆，记为第3个半圆；以DE＝8为直径画半圆，记为第4个半圆；···，按此规律，继续画半圆，则第6个半圆的面积为______________．（结果保留π）
粤公网安备 44130202000953号