为改善购物环境,提高经济效益,某商场决定投资800万元改造商场内部环境,据调查,改造好购物环境后,任何一个月内(每月按30天计算)每天的顾客人数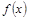 与第x天近似地满足
与第x天近似地满足 (千人),且每位顾客人均购物金额数
(千人),且每位顾客人均购物金额数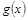 近似地满足
近似地满足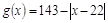 (元).
(元).
(1)求该商场第x天的销售收入 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,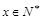 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天纯收入的计量依据,商场决定以每日纯收入的5%收回投资成本,试问商场在两年内能否收回全部投资成本.
推荐套卷
为改善购物环境,提高经济效益,某商场决定投资800万元改造商场内部环境,据调查,改造好购物环境后,任何一个月内(每月按30天计算)每天的顾客人数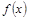 与第x天近似地满足
与第x天近似地满足 (千人),且每位顾客人均购物金额数
(千人),且每位顾客人均购物金额数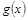 近似地满足
近似地满足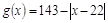 (元).
(元).
(1)求该商场第x天的销售收入 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,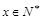 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天纯收入的计量依据,商场决定以每日纯收入的5%收回投资成本,试问商场在两年内能否收回全部投资成本.