在用数学归纳法证明f(n)= +
+ +…+
+…+ <1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
<1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
A. + +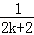 |
B. + +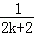 ﹣ ﹣ |
C.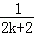 ﹣ ﹣ |
D.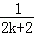 ﹣ ﹣ |
相关知识点
推荐套卷
在用数学归纳法证明f(n)= +
+ +…+
+…+ <1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
<1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
A. + +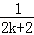 |
B. + +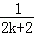 ﹣ ﹣ |
C.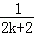 ﹣ ﹣ |
D.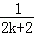 ﹣ ﹣ |