（本小题满分12分）我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图，“盾圆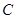
”是由椭圆
与抛物线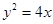
中两段曲线合成，
为椭圆左、右焦点，
，
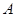为椭圆与抛物线的一个公共点，
.
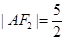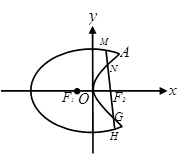
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在过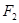
的一条直线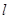
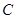，与“盾圆”依次交于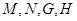
四点，使得
与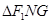
的面积之比为
，若存在，求出直线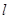的方程；若不存在，说明理由.
并且与曲线
相切的直线方程。
中，满足
,
是
边上的一点.
,求向量
与向量
夹角的正弦值；
，
=m (m为正常数) 且
值；
且
求
的最小值。推荐套卷
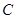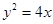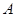（本小题满分12分）我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图，“盾圆”是由椭圆与抛物线中两段曲线合成，为椭圆左、右焦点，，为椭圆与抛物线的一个公共点，.
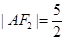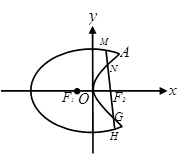
（Ⅰ）求椭圆的方程；
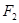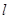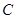（Ⅱ）是否存在过的一条直线，与“盾圆”依次交于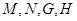四点，使得与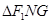的面积之比为，若存在，求出直线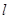的方程；若不存在，说明理由.
粤公网安备 44130202000953号