已知抛物线y="Ax" 2 +Bx+C与y轴交于点A(0,3),与x轴分别交于B(1,0)、C(5,0)两点.
(1)求此抛物线的解析式;
(2)若点D为线段OA的一个三等分点,求直线DC的解析式;
(3)若一个动点P自OA的中点M出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A.求使点P运动的总路径最短的点E、点F的坐标,并求出这个最短总路径的长.
(4)若点N的坐标为(3,4),Q为x轴上一点,△ONQ为等腰三角形,请直接写出点Q的坐标。
相关知识点
推荐套卷
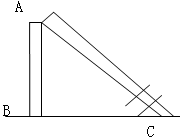
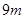 处决裂,旗杆顶部落在离旗杆底部12m处,旗杆折断之前有多高?
处决裂,旗杆顶部落在离旗杆底部12m处,旗杆折断之前有多高?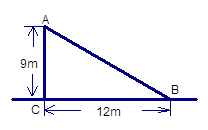
 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方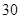 m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为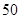 m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?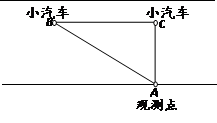
 粤公网安备 44130202000953号
粤公网安备 44130202000953号