给定下列两个关于异面直线的命题:那么( )
命题(1):若平面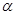 上的直线
上的直线 与平面
与平面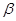 上的直线
上的直线 为异面直线,直线
为异面直线,直线 是
是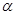 与
与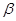 的交线,那么
的交线,那么 至多与
至多与 中的一条相交;
中的一条相交;
命题(2):不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
| A.命题(1)正确,命题(2)不正确 |
| B.命题(2)正确,命题(1)不正确 |
| C.两个命题都正确 |
| D.两个命题都不正确 |
推荐套卷
给定下列两个关于异面直线的命题:那么( )
命题(1):若平面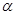 上的直线
上的直线 与平面
与平面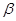 上的直线
上的直线 为异面直线,直线
为异面直线,直线 是
是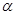 与
与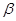 的交线,那么
的交线,那么 至多与
至多与 中的一条相交;
中的一条相交;
命题(2):不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
| A.命题(1)正确,命题(2)不正确 |
| B.命题(2)正确,命题(1)不正确 |
| C.两个命题都正确 |
| D.两个命题都不正确 |