为适应2012年3月23日公安部交通管理局印发的《加强机动车驾驶人管理指导意见》,某驾校将小型汽车驾照考试科目二的培训测试调整为:从10个备选测试项目中随机抽取4个,只有选中的4个项目均测试合格,科目二的培训才算通过.已知甲对10个测试项目测试合格的概率均为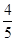 ;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
(1)求甲恰有2个测试项目合格的概率;
(2)记乙的测试项目合格数为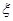 ,求
,求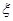 的分布列及数学期望
的分布列及数学期望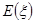 .
.
推荐套卷
为适应2012年3月23日公安部交通管理局印发的《加强机动车驾驶人管理指导意见》,某驾校将小型汽车驾照考试科目二的培训测试调整为:从10个备选测试项目中随机抽取4个,只有选中的4个项目均测试合格,科目二的培训才算通过.已知甲对10个测试项目测试合格的概率均为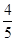 ;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
(1)求甲恰有2个测试项目合格的概率;
(2)记乙的测试项目合格数为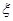 ,求
,求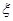 的分布列及数学期望
的分布列及数学期望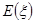 .
.