已知:如图,等腰直角三角形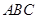 的直角边
的直角边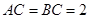 ,沿其中位线
,沿其中位线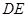 将平面
将平面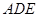 折起,使平面
折起,使平面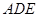 ⊥平面
⊥平面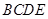 ,得到四棱锥
,得到四棱锥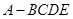 ,设
,设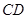 、
、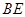 、
、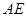 、
、 的中点分别为
的中点分别为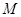 、
、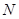 、
、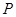 、
、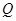 .
.


(1)求证: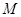 、
、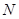 、
、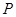 、
、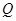 四点共面;
四点共面;
(2)求证:平面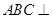 平面
平面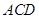 ;
;
(3)求异面直线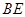 与
与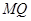 所成的角.
所成的角.
相关知识点
推荐套卷
已知:如图,等腰直角三角形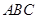 的直角边
的直角边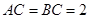 ,沿其中位线
,沿其中位线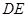 将平面
将平面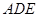 折起,使平面
折起,使平面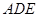 ⊥平面
⊥平面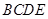 ,得到四棱锥
,得到四棱锥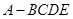 ,设
,设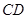 、
、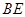 、
、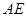 、
、 的中点分别为
的中点分别为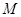 、
、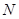 、
、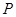 、
、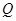 .
.


(1)求证: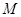 、
、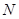 、
、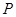 、
、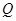 四点共面;
四点共面;
(2)求证:平面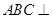 平面
平面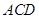 ;
;
(3)求异面直线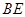 与
与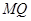 所成的角.
所成的角.