已知函数f(x)＝ax3＋|x－a|，a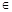
R．
（1）若a＝－1，求函数y＝f(x) (x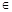 [0，＋∞))的图象在x＝1处的切线方程；
（2）若g(x)＝x4，试讨论方程f(x)＝g(x)的实数解的个数；
（3）当a＞0时，若对于任意的x1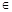 [a，a＋2]，都存在x2 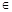[a＋2，＋∞)，使得f(x1)f(x2)＝1024，求满足条件的正整数a的取值的集合．
，
，
，其中
，
，
与
的夹角
，
与
，且
，求
的值。
，
，
，
。
是否共线？请说
明理由。
的最大值。
中，已知
，推荐套卷
已知函数f(x)＝ax3＋|x－a|，a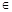R．
（1）若a＝－1，求函数y＝f(x) (x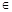 [0，＋∞))的图象在x＝1处的切线方程；
（2）若g(x)＝x4，试讨论方程f(x)＝g(x)的实数解的个数；
（3）当a＞0时，若对于任意的x1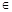 [a，a＋2]，都存在x2 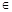[a＋2，＋∞)，使得f(x1)f(x2)＝1024，求满足条件的正整数a的取值的集合．
粤公网安备 44130202000953号