如图，在所给方格纸中，每个小正方形边长都是1，标号为①，②，③的三个三角形均为格点三角形（顶点在方格顶点处）.请按要求将图甲、图乙中的指定图形分割成三个三角形，使它们与标号为①，②，③的三个三角形分别对应全等.
（1）图甲中的格点正方形ABCD；
（2）图乙中的平行四边形ABCD.
注：图甲、图乙在答题卡上，分割线画成实线.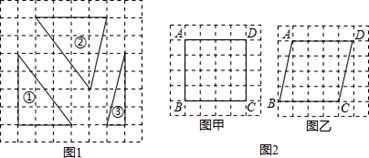
相关试题
+（-
）
（4）-
ABCD，E，F是对角线BD所在直线上的两点，且AE∥CF，求证：CE∥AF．
ABCD，E， F是对角线BD上的两点，且DE=BF.
相关知识点
推荐套卷
如图，在所给方格纸中，每个小正方形边长都是1，标号为①，②，③的三个三角形均为格点三角形（顶点在方格顶点处）.请按要求将图甲、图乙中的指定图形分割成三个三角形，使它们与标号为①，②，③的三个三角形分别对应全等.
（1）图甲中的格点正方形ABCD；
（2）图乙中的平行四边形ABCD.
注：图甲、图乙在答题卡上，分割线画成实线.
粤公网安备 44130202000953号