如图，在矩形ABCD中，AB=4cm，BC=8cm．点P从点D出发向点A运动，运动到点A即停止；同时点Q从点B出发向点C运动，运动到点C即停止．点P、Q的速度都是1cm/s．连结PQ，AQ，CP.设点P、Q运动的时间为t（s）.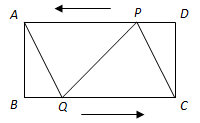
（1）当t为何值时，四边形ABQP是矩形．
（2）当t为何值时，四边形AQCP是菱形．
（3）分别求出（2）中菱形AQCP的周长和面积．
相关试题
与方程组
的解相同，求m、n的值．
．相关知识点
推荐套卷
如图，在矩形ABCD中，AB=4cm，BC=8cm．点P从点D出发向点A运动，运动到点A即停止；同时点Q从点B出发向点C运动，运动到点C即停止．点P、Q的速度都是1cm/s．连结PQ，AQ，CP.设点P、Q运动的时间为t（s）.
（1）当t为何值时，四边形ABQP是矩形．
（2）当t为何值时，四边形AQCP是菱形．
（3）分别求出（2）中菱形AQCP的周长和面积．
粤公网安备 44130202000953号