若曲线f（x，y）=0上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0的“自公切线”，下列方程：
①x2﹣y2=1
②x2﹣|x﹣1|﹣y=0
③xcosx﹣y=0
④|x|﹣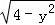
+1=0
其中所对应的曲线中存在“自公切线”的有（ ）
| A．①② | B．②③ | C．①④ | D．③④ |
，
则集合B不可能是（ ）
与直线
互相垂直，那么
的值等于（ ）
在
轴上的截距是（ ）
的真子集总共有（ ）相关知识点
推荐套卷
若曲线f（x，y）=0上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0的“自公切线”，下列方程：
①x2﹣y2=1
②x2﹣|x﹣1|﹣y=0
③xcosx﹣y=0
④|x|﹣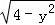+1=0
其中所对应的曲线中存在“自公切线”的有（ ）
| A．①② | B．②③ | C．①④ | D．③④ |
粤公网安备 44130202000953号